Poroelasticity refers to the coupling between mechanical deformation and fluid flow and is a process that is ubiquitous to the geosciences. Within crustal properties alone, poromechanics provide a governing framework to describe the processes behind subsurface hydrology, petroleum reservoirs and production, seismic activity, carbon capture and storage, and geothermal energy.
Prior efforts to incorporate poroelasticity within the PyLith framework have relied on a coupled approach1 employing a separate reservoir simulator in conjunction with the mechanical modeling capability built into PyLith. While permitting a specialized and refined means of modeling flow, this effectively required the consideration of two separate problems, with two separate modeling domains, and two separate means of simulation input. In addition, the iterative transfer of information between two separate models for fluid flow and mechanics reduced the ability for solver optimization.
With the upcoming version of PyLith, we have leveraged the new design to allow for the representation of multiphysics within what was formerly solely a mechanics code. This permits the solver flexibility and domain decomposition capabilities of the PETSc package, serving as the mathematical engine of PyLith, to be applied to the entire modeled domain.
Modeling linear poroelastic behavior has served as an initial test run for this new capability. To check our performance, we use well established benchmarks that have known analytical solutions. One such example is Cryer’s problem,2 demonstrated here (Figure 1). This problem models a fluid saturated porous sphere subjected to an instantaneous radial compressive stress. Even though the surface is considered as a permeable interface at drained conditions, an internal rise in pore pressure is observed (Figure 2). This non-monotonic pressure diffusion is known as the Mandel-Cryer effect (Figure 3). Owing to symmetry, this problem may be represented by modeling an eighth of the entire domain and setting normal boundary displacement to zero.
Currently in active development is a poroelastic fault model based upon the formulation given by Cocco and Rice,3 to go along with the linear poroelastic physics implemented for the bulk domain. Further information on the incorporation of poroelasticity into PyLith can be found in the forthcoming paper.4
Contributed by:
Robert Walter, SUNY Buffalo; Brad Aagaard, USGS; and Matt Knepley, SUNY Buffalo
References
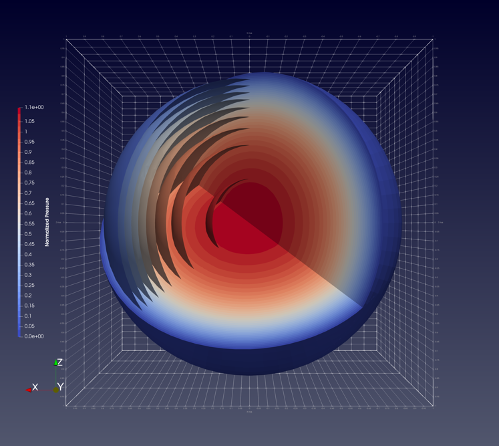
Figure 1. Representation of Cryer's problem at the normalized time step t* = 0.04186. The pressure at the surface is maintained at a drained condition (zero), while constant compressive force is applied on the same boundary. The entire spherical problem is modeled, with the contours representing steps in the normalized pressure values.
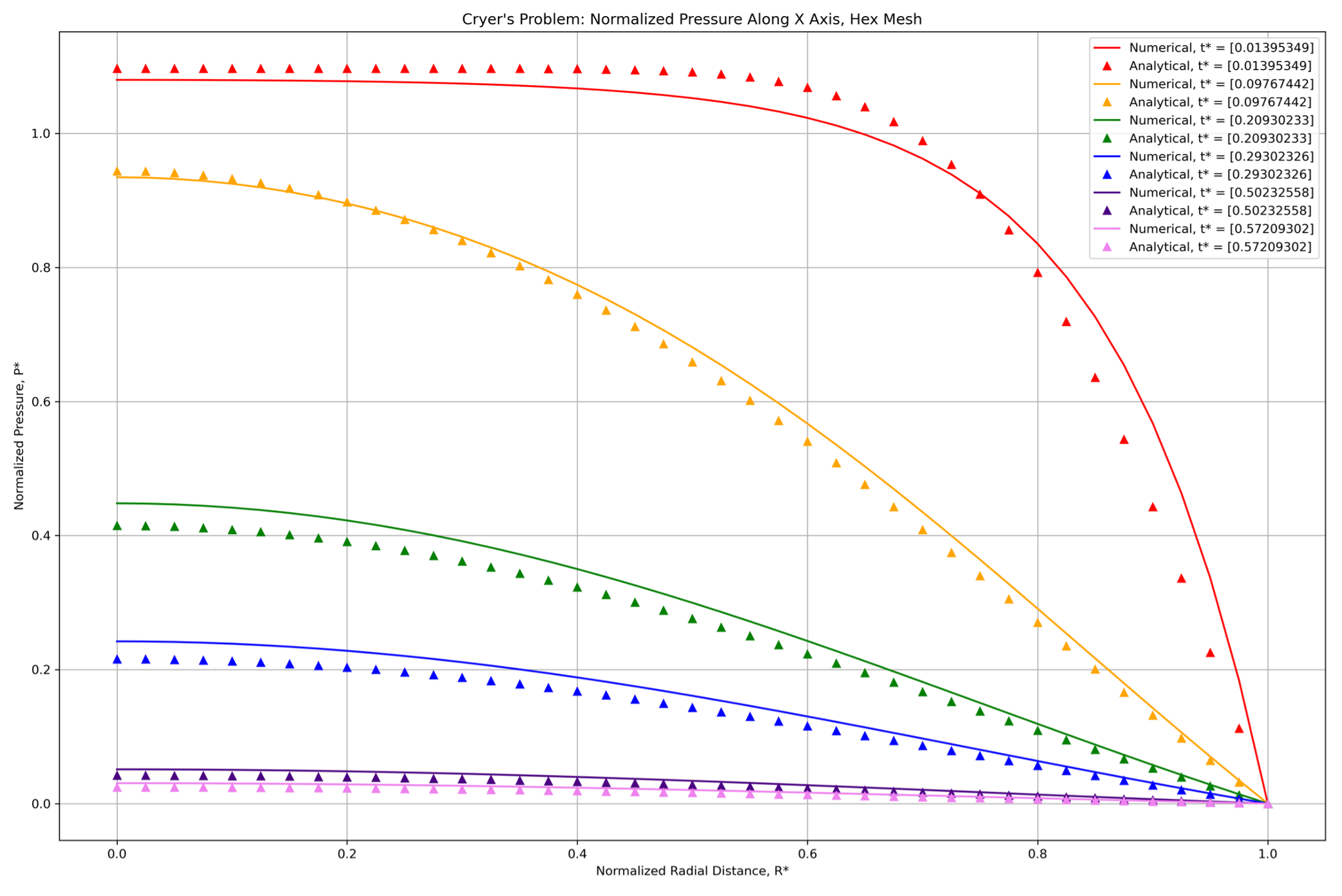
Figure 2. Figure displaying the normalized pressure along an axis versus normalized radial distance. As the sphere is radially isotropic, any direction will be functionally equivalent, and a coordinate axis is chosen for simplicity. Calculated analytical solution values are represented by triangles, color coded with respect to the normalized time for that particular iteration.
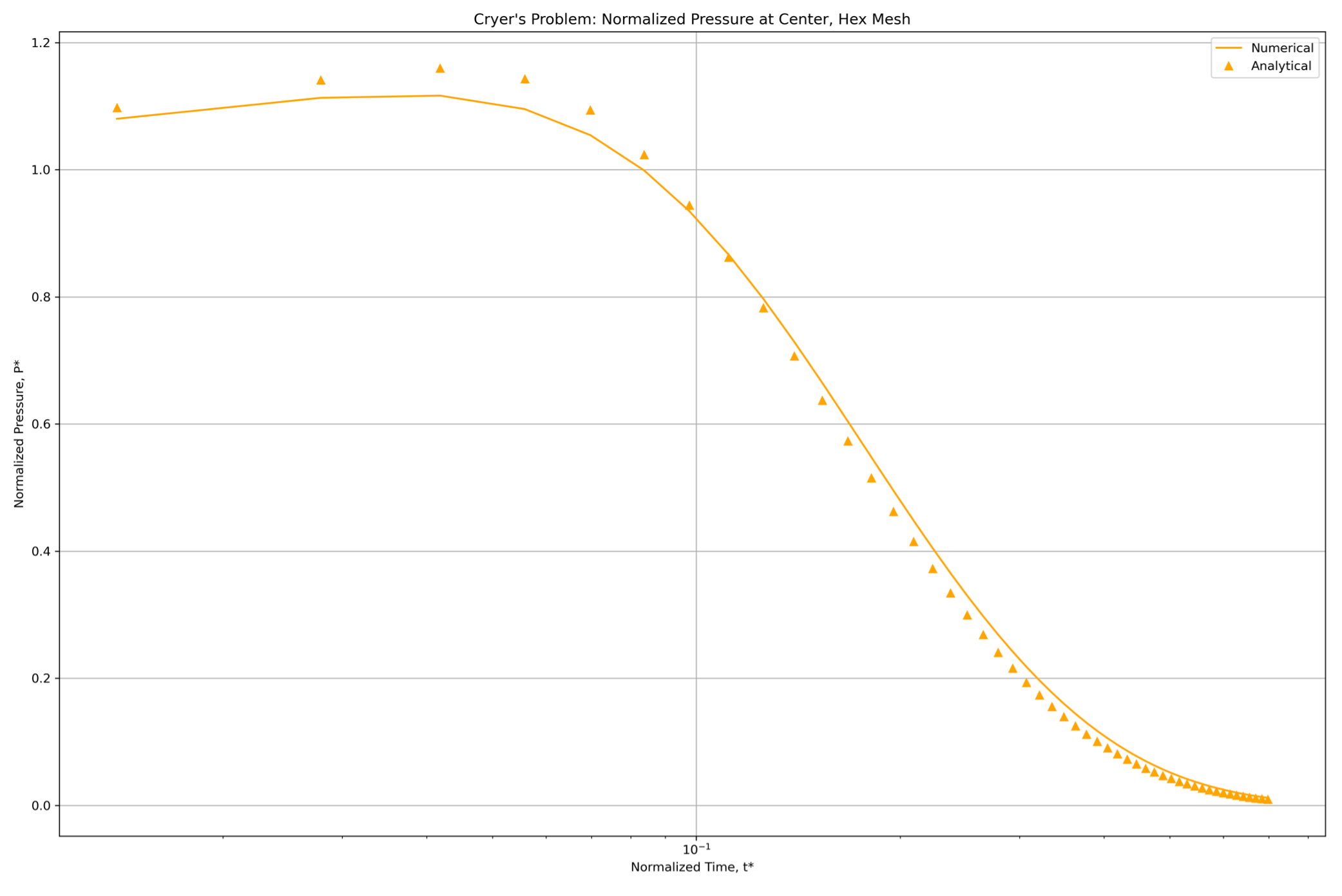
Figure 3. Graph of normalized pressure at the origin of the sphere versus normalized time. The initial rise in pressure indicative of the Mandel-Cryer effect can be observed.